A)
B)
C)
D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Solve the problem. -A ladder that is 13 feet long is 5 feet from the base of a wall. How far up the wall does the ladder reach?
A) 144 ft
B)
C)
D) 12 ft
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Solve the inequality and give the solution in interval notation. -(x +x 1+) (x 10- 3) ? 0
A)
B)
C)
D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find all x-intercepts of the function. -
A) (10, 0) , (4, 0)
B) (100, 0) , (16, 0)
C)
D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Solve the problem. -The accumulative number of vehicles passing over a bridge during rush hour is given by the formulahe formula where C is the number of vehicles and t is the minutes past . At what time will 578 vehicles have passed over the bridge?
A) 7:17 A.M.
B) 7:20 A.M.
C) 7:23 A.M.
D) 7:18 A.M.
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the vertex and axis of symmetry of the graph of the function. -
A) vertex: (0, 1) ; x = 0
B) vertex: (1, 0) ; x = 1
C) vertex: (-1, 0) ; x = -1
D) vertex: (0, -1) ; x = 0
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Solve the equation. -
A) -5
B) -4
C) 6
D) 5
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the x-intercepts (if any) of the graph of the function. If the x-intercepts are irrational, round your answers to the nearest tenth. -
A) x-intercepts: (5, 0) and (6, 0)
B) x-intercepts: (5, 0) and (-6, 0)
C) x-intercepts: (-5, 0) and (-6, 0)
D) No x-intercepts
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Solve the equation by the quadratic formula. -
A)
B)
C)
D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Solve the equation. -
A)
B)
C) 6, 3
D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
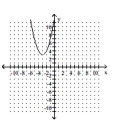
Match the graph with the appropriate function.
-
A)
B)
C)
D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Solve the problem. -The length of a vegetable garden is 6 feet longer than its width. If the area of the garden is 112 square feet, find its dimensions.
A) w = 7 ft; l = 15 ft
B) w = 9 ft; l = 15 ft
C) w = 7 ft; l = 13 ft
D) w = 8 ft; l = 14 ft
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Determine whether the parabola opens upward or downward. -
A) downward
B) upward
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Solve the inequality and give the solution set in set builder notation. -
A)
B)
C)
D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Solve the problem. -The formula represents the number of households N, in thousands, in a certain city that have a computer x years after 1990. According to the formula, in what year were there 164 thousand households with Computers in this city?
A) 1995
B) 1996
C) 1997
D) 1994
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Write an equation that has the given solutions. -
A)
B)
C)
D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Solve the equation by the quadratic formula. -
A)
B)
C)
D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Solve the problem. -The product of a number and 3 less than the number is 18. Find the number.
A) -6 or 3
B) -7 or 2
C) -3 or 6
D) -2 or 7
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Solve the inequality and graph the solution on a number line.
-

A) ![]()
B) ![]()
C) ![]()
![]()
D) ![]()
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Solve for the indicated variable. Assume the variable you are solving for must be greater than 0. -A
A)
B)
C)
D)
Correct Answer

verified
Correct Answer
verified
Showing 61 - 80 of 221
Related Exams