A) 2 - ![]() square units
square units
B) 2 + ![]() square units
square units
C) - ![]() square units
square units
D) + ![]() square units
square units
E) ![]() -
- ![]() square units
square units
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the equation of the parabola whose focus is (2, -1) and directrix is x + 2y -1 = 0.
A) 4x2 - 4xy + y2 -18x + 14y + 24 = 0
B) 5x2 - 4xy + y2 -18x + 14y + 24 = 0
C) x2 - 4xy + 4y2 -18x + 14y + 24 = 0
D) x2 - 4xy + 5y2 -18x + 14y + 24 = 0
E) 4x2 - 4xy + 4y2 -18x + 14y + 24 = 0
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the arc length of r = 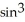
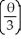 from = 0 to =
from = 0 to = 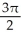 .
.
A) ![]() units
units
B) ![]() units
units
C) ![]() units
units
D) ![]() units
units
E) ![]() units
units
Correct Answer

verified
Correct Answer
verified
Multiple Choice
The equations x(t) = 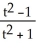 , y(t) =
, y(t) = 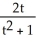 , -1 t 1 are the parametric equations of
, -1 t 1 are the parametric equations of
A) the whole circle centred at (0 , 0) and is of radius 1 unit
B) the left half of the circle centred at (0 , 0) and is of radius 1 unit
C) the bottom half of the circle centred at (0 , 0) and is of radius 1 unit
D) the top half of the circle centred at (0 , 0) and is of radius 1 unit
E) the right half of the circle centred at (0 , 0) and is of radius 1 unit
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the length of r = 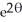 from = 0 to = 2 .
from = 0 to = 2 .
A) ![]() (
( ![]() - 1) units
- 1) units
B) ![]() (
( ![]() - 1) units
- 1) units
C) ![]() (
( ![]() - 1) units
- 1) units
D) 2 ![]() (
( ![]() - 1) units
- 1) units
E) ![]() (
( ![]() + 1) units
+ 1) units
Correct Answer

verified
Correct Answer
verified
Essay
Sketch the polar curve r = 4 sin(3θ).
Correct Answer

verified
Correct Answer
verified
True/False
If x = f( ) cos( ), y = f( ) sin( ) for ![If x = f( \theta ) cos( \theta ), y = f( \theta ) sin( \theta ) for \theta [ , ] , are parametric equations of a plane curve C, then the equation of curve C in polar coordinates is r = f( \theta ), \theta 1ee7b17_3372_5854_ae82_d19d2ea0c252_TB9661_11 [ , ].](https://d2lvgg3v3hfg70.cloudfront.net/TB9661/11ee7b17_3372_5854_ae82_d19d2ea0c252_TB9661_11.jpg) [
[![If x = f( \theta ) cos( \theta ), y = f( \theta ) sin( \theta ) for \theta [ , ] , are parametric equations of a plane curve C, then the equation of curve C in polar coordinates is r = f( \theta ), \theta 1ee7b17_3372_5854_ae82_d19d2ea0c252_TB9661_11 [ , ].](https://d2lvgg3v3hfg70.cloudfront.net/TB9661/11ee7b18_881f_7ad5_ae82_ef6a0704a9e3_TB9661_11.jpg) ,
, ![If x = f( \theta ) cos( \theta ), y = f( \theta ) sin( \theta ) for \theta [ , ] , are parametric equations of a plane curve C, then the equation of curve C in polar coordinates is r = f( \theta ), \theta 1ee7b17_3372_5854_ae82_d19d2ea0c252_TB9661_11 [ , ].](https://d2lvgg3v3hfg70.cloudfront.net/TB9661/11ee7b18_ef83_6016_ae82_a1fef198316c_TB9661_11.jpg) ] , are parametric equations of a plane curve C, then the equation of curve C in polar coordinates is r = f( ), 1ee7b17_3372_5854_ae82_d19d2ea0c252_TB9661_11 [11ee7b18_881f_7ad5_ae82_ef6a0704a9e3_TB9661_11 , 11ee7b18_ef83_6016_ae82_a1fef198316c_TB9661_11].
] , are parametric equations of a plane curve C, then the equation of curve C in polar coordinates is r = f( ), 1ee7b17_3372_5854_ae82_d19d2ea0c252_TB9661_11 [11ee7b18_881f_7ad5_ae82_ef6a0704a9e3_TB9661_11 , 11ee7b18_ef83_6016_ae82_a1fef198316c_TB9661_11].
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Determine the coordinates of the points where the curve x =  + 2t, y = 2
+ 2t, y = 2 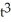 + 7 has (a) a horizontal tangent and (b) a vertical tangent.
+ 7 has (a) a horizontal tangent and (b) a vertical tangent.
A) (a) (0, -9) (b) (±2, -6)
B) (a) (-2, -9) (b) (-2, -6)
C) (a) (2, -9) (b) (2, -6)
D) (a) (0, -9) (b) (2, 6)
E) (a) (2, 9) (b) (2, 6)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the arc length x = 2 cos + cos 2 + 1, y = 2 sin + sin 2 , for 0 2 .
A) 12 units
B) 14 units
C) 16 units
D) 18 units
E) 10 units
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the Cartesian equation of the straight line tangent to the plane curve given parametrically by  at the point on the curve where t = -1.
at the point on the curve where t = -1.
A) x + y = 0
B) 3x - y =0
C) y = 0
D) y = ![]() x
x
E) y = -3x
Correct Answer

verified
Correct Answer
verified
Essay
The equation of a conic section in polar coordinates is given by r = 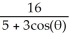 .(i) Transform the equation of the conic section to rectangular coordinates (x , y).(ii) Identify the conic section.
.(i) Transform the equation of the conic section to rectangular coordinates (x , y).(ii) Identify the conic section.
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find g(t) so that x = -1 + 3 cos(t) , y = g(t) , 0 t 2 provides a counterclockwise parametrization of the circle 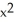 +
+ 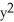 + 2x - 4y = 4.
+ 2x - 4y = 4.
A) -2 + sin(t)
B) 2 - 3 sin(t)
C) 2 + 3 sin(t)
D) 3 - 2 sin(t)
E) 3 + 2 sin(t)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Convert the point with Cartesian coordinates (-1, -1) to polar coordinates.
A) ![]()
B) ![]()
C) ![]()
D) ![]()
E) ![]()
Correct Answer

verified
Correct Answer
verified
Multiple Choice
For the parabola 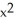 + 6x + 4y + 5 = 0, find the vertex, the focus, and the directrix.
+ 6x + 4y + 5 = 0, find the vertex, the focus, and the directrix.
A) Vertex (3, 1) , Focus (3, 2) , Directrix y = 0
B) Vertex (3, 1) , Focus (3, 0) , Directrix y = 2
C) Vertex (-3, 1) , Focus (-3, 2) , Directrix y = 0
D) Vertex (-3, 1) , Focus (-3, 0) , Directrix y = 2
E) Vertex (-3, -1) , Focus (-3, 0) , Directrix y = 2
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Transform the polar equation r = 1 + 2 cos to rectangular coordinates.
A) ![]() +
+ ![]() =
= ![]()
B) ![]() +
+ ![]() =
= ![]()
C) ![]() -
- ![]() =
= ![]()
D) ![]() +
+ ![]() =
= ![]()
E) ![]() -
- ![]() =
= ![]()
Correct Answer

verified
Correct Answer
verified
Multiple Choice
A conic section is given by the equation 4x2 + 10xy + 4y2 = 36.Use rotation of coordinate axes through an appropriate acute angle to find the new equation of the conic section in the uv-coordinate axes , where x = u cos( ) - v sin( ) , y = u sin( ) + v cos( ) . Then identify the conic section.
A) ![]() +
+ ![]() = 1, an ellipse
= 1, an ellipse
B) ![]() +
+ ![]() = 4, a circle
= 4, a circle
C) ![]() -
- ![]() = 1, a hyperbola
= 1, a hyperbola
D) ![]() +
+ ![]() = 1, an ellipse
= 1, an ellipse
E) ![]() -
- ![]() = 1, a hyperbola
= 1, a hyperbola
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find an equation of a parabola satisfying the given conditions: Focus (2, 0) and directrix y = 2?.
A) ![]() = 4 (1 - y)
= 4 (1 - y)
B) ![]() = 4( - y)
= 4( - y)
C) ![]() = 4 ( - y)
= 4 ( - y)
D) ![]() = 4 ( - y)
= 4 ( - y)
E) ![]() = 4 ( - y)
= 4 ( - y)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the area bounded by the polar curve r = sin(3 ) .
A) ![]() square units
square units
B) ![]() square units
square units
C) ![]() square units
square units
D) ![]() square units
square units
E) ![]() square units
square units
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Express 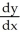 and
and 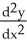 in terms of x and y for the circle x = a cos
, y = a sin
.
in terms of x and y for the circle x = a cos
, y = a sin
.
A) ![]() = -
= - ![]() ,
, ![]() = -
= - ![]()
B) ![]() =
= ![]() ,
, ![]() =
= ![]()
C) ![]() = -
= - ![]() ,
, ![]() = -
= - ![]()
D) ![]() =
= ![]() ,
, ![]() = -
= - ![]()
E) ![]() =
= ![]() ,
, ![]() = -
= - ![]()
Correct Answer

verified
Correct Answer
verified
Multiple Choice
What are the polar coordinates of the highest point on the cardioid r = 2(1 + cos ) ?
A) ![]()
B) ![]()
C) ![]()
D) (4, 0)
E) ![]()
Correct Answer

verified
Correct Answer
verified
Showing 61 - 80 of 114
Related Exams