A) Pr(J or Q or K) = ![]()
B) Pr(J or Q or K) = ![]()
C) Pr(Jor Q or K) = ![]()
D) Pr(J or Q or K) = ![]()
E) Pr(J or Q or K) = ![]()
Correct Answer

verified
Correct Answer
verified
Multiple Choice
A bag contains 7 white balls and 8 red balls. Construct a probability tree to determine the probability that if 2 balls are drawn,with replacement, the first ball is red R and the second is white W.
A) Pr(R first ∩ W second) = ![]()
B) Pr(R first ∩ W second) = ![]()
C) Pr(R first ∩ W second) = ![]()
D) Pr(R first ∩ W second) = ![]()
E) Pr(R first ∩ W second) = ![]()
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Use the transition matrix  and initial probability vector
and initial probability vector 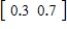 to find the resulting third probability vector. Round all numerical values in your answer to three decimal places.
to find the resulting third probability vector. Round all numerical values in your answer to three decimal places.
A) ![]()
B) ![]()
C) ![]()
D) ![]()
E) ![]()
Correct Answer

verified
Correct Answer
verified
Multiple Choice
An unprepared student must take a 7-question, multiple-choice test that has 5 possible answers per question. If the student can eliminate two of the possible answers on the first three questions, and if she guesses on every question, what is the probability that she will answer at least one question correctly?
A) Pr(at least 1 correct) = ![]()
B) Pr(at least 1 correct) = ![]()
C) Pr(at least 1 correct) = ![]()
D) Pr(at least 1 correct) = ![]()
E) Pr(at least 1 correct) = ![]()
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Thirty-seven percent of the cars owned by a car rental firm have some defect. What is the probability that if 3 cars are selected at random, at least one would have a defect? Round your answer to four decimal places.
A) 0.0507
B) 0.2500
C) 0.7500
D) 0.6031
E) 0.8425
Correct Answer

verified
Correct Answer
verified
Multiple Choice
According to a recent medical study, 196 of 200 mammograms turn out to be normal. What is the probability that the mammogram of a woman chosen at random will show an abnormality?
A) Pr(abnormality) = ![]()
B) Pr(abnormality) = 196
C) Pr(abnormality) = 4
D) Pr(abnormality) = ![]()
E) Pr(abnormality) = ![]()
Correct Answer

verified
Correct Answer
verified
Multiple Choice
A company estimates that 50% of the country has seen its commercial and that if a person sees its commercial, there is a 45% probability that the person will buy its product. What is the probability that a person chosen at random in the country will have seen the commercial and bought the product? Round your answer to four decimal places.
A) 0.0111
B) 0.0500
C) 0.4500
D) 0.5000
E) 0.2250
Correct Answer

verified
Correct Answer
verified
Multiple Choice
A red ball and 17 white balls are in a box. If two balls are drawn, without replacement, what is the probability of getting 2 red R balls?
A) Pr(R first ∩ R second) = 1
B) Pr(R first ∩ R second) = ![]()
C) Pr(R first ∩ R second) = ![]()
D) Pr(R first ∩ R second) = ![]()
E) Pr(R first ∩ R second) = 0
Correct Answer

verified
Correct Answer
verified
Multiple Choice
If the odds that a particular horse will win a race are 15 : 9, what is the probability that the horse will win the race?
A) ![]()
B) ![]()
C) ![]()
D) ![]()
E) ![]()
Correct Answer

verified
Correct Answer
verified
Multiple Choice
To see whether a bank has enough minority construction company loans, a social agency selects 31 loans to construction companies at random and finds that 4 of them are loans to minority companies. If the bank's claim that 10 of every 100 of its loans to construction companies are minority loans is true, what is the probability that 4 loans out of 31 are minority loans? Leave your answer with combination symbols.
A) ![]()
B) ![]()
C) ![]()
D) ![]()
E) ![]()
Correct Answer

verified
Correct Answer
verified
Multiple Choice
A mathematics class consists of 14 engineering majors E, 8 science majors S, and 15 liberal arts majors LA. What is the probability that a student selected at random will be an engineering or science major?
A) Pr(E∪S) = ![]()
B) Pr(E∪S) = ![]()
C) Pr(E∪S) = ![]()
D) Pr(E∪S) = ![]()
E) Pr(E∪S) = ![]()
Correct Answer

verified
Correct Answer
verified
Multiple Choice
An urn contains 8 red, 9 white, and 2 black balls. One ball is drawn from the urn, it is replaced, and a second ball is drawn. Construct a probability tree to determine the probability that at least one ball drawn is black B.
A) Pr(at least one B) = ![]()
B) Pr(at least one B) = ![]()
C) Pr(at least one B) = ![]()
D) Pr(at least one B) = ![]()
E) Pr(at least one B) = ![]()
Correct Answer

verified
Correct Answer
verified
Multiple Choice
The following table gives the percent of employees of the Ace Company in each of three salary brackets, categorized by the sex of the employees. An employee is selected at random. What is the probability that the person selected is female and makes less than $30,000?
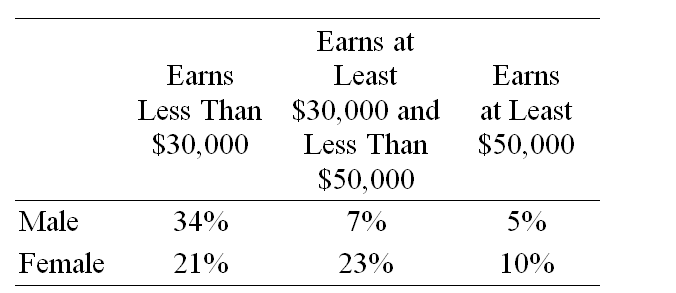
A) Pr(female∩less than $30,000) = 0.34
B) Pr(female∩less than $30,000) = 0.21
C) Pr(female∩less than $30,000) = 0.54
D) Pr(female∩less than $30,000) = 0.55
E) Pr(female∩less than $30,000) = 0.33
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Two balls are drawn, without replacement, from a bag containing 18 blue balls numbered 1-18 and 4 green balls numbered 19-22. What is the probability that the first ball is blue and even-numbered and the second ball is even-numbered?
A) ![]()
B) ![]()
C) 0
D) ![]()
E) ![]()
Correct Answer

verified
Correct Answer
verified
Multiple Choice
A fair die is rolled. Find the probability that the result is a 4, given that the result is even.
A) ![]()
B) ![]()
C) ![]()
D) ![]()
E) 0
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Six men and four women are semifinalists in a lottery. From this group, three finalists are to be selected by a drawing. What is the probability that all four finalists will be men? Round your answer to three decimal places.
A) 0.071
B) 0.571
C) 0.005
D) 0.667
E) 0.600
Correct Answer

verified
Correct Answer
verified
Multiple Choice
From a deck of 52 playing cards, two cards are drawn, one after the other without replacement. What is the probability that the first will be an ace nd the second will be an ace?
A) ![]()
B) ![]()
C) ![]()
D) ![]()
E) ![]()
Correct Answer

verified
Correct Answer
verified
Multiple Choice
A bag contains 4 red balls and 11 white balls. Two balls are drawn from the bag. What is the probability that the second ball is white W, given that the first ball is red and is replaced before the second is drawn?
A) Pr(W) = ![]()
B) Pr(W) = ![]()
C) Pr(W) = ![]()
D) Pr(W) = ![]()
E) Pr(W) = ![]()
Correct Answer

verified
Correct Answer
verified
Multiple Choice
An examination consists of 11 questions. If 6 questions must be answered, find the number of different orders in which a student can answer the questions.
A) 151,200
B) 332,640
C) 17
D) 66
E) 1,771,561
Correct Answer

verified
Correct Answer
verified
Multiple Choice
An urn contains three red R balls numbered 1, 2 and 3, four white W balls numbered 4, 5, 6 and 7, and three black B balls numbered 8, 9 and 10. A ball is drawn from the urn. What is the probability that it is red?
A) P(R) = ![]()
B) P(R) = ![]()
C) P(R) = ![]()
D) P(R) = ![]()
E) P(R) = ![]()
Correct Answer

verified
Correct Answer
verified
Showing 41 - 60 of 180
Related Exams