Correct Answer

verified
Correct Answer
verified
Essay
Let . (a) Sketch the graph of . (b) Find the domain of . (c) State the intervals on which is increasing and on which is decreasing.
Correct Answer

verified
(a) 
(b) D...View Answer
Show Answer
Correct Answer
verified
(b) D...
View Answer
Essay
Find the inverse function of , .
Correct Answer

verified




 , but...
, but...View Answer
Show Answer
Correct Answer
verified
View Answer
Essay
Determine whether or not the function is one-to-one.
Correct Answer

verified

Two different positive numbers cannot h...View Answer
Show Answer
Correct Answer
verified
Two different positive numbers cannot h...
View Answer
Essay
Let and . Find , , and their domains.
Correct Answer

verified
 , domain ...
, domain ...View Answer
Show Answer
Correct Answer
verified
View Answer
Essay
Graphs of the functions f and g are given.
(a) Which is larger,
(b) Which is larger,
(c) For which values of x is
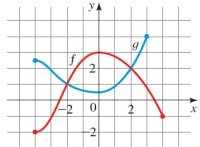
Correct Answer

verified
Correct Answer
verified
Essay
Find the inverse function of , .
Correct Answer

verified
Correct Answer
verified
Essay
If and , find , , and their domains.
Correct Answer

verified
 , domain ...
, domain ...View Answer
Show Answer
Correct Answer
verified
View Answer
Essay
Given , , and , find .
Correct Answer

verified
Correct Answer
verified
Essay
If and , find , , and their domains.
Correct Answer

verified
 , domain ...
, domain ...View Answer
Show Answer
Correct Answer
verified
View Answer
Essay
If and , find , , and their domains.
Correct Answer

verified
 , domain ...
, domain ...View Answer
Show Answer
Correct Answer
verified
View Answer
Essay
Let , (a) Sketch the graph of then use it to sketch the graph of . (b) Find .
Correct Answer

verified


 . So th...
. So th...View Answer
Show Answer
Correct Answer
verified
View Answer
Essay
Let . (a) Sketch the graph of . (b) Find the domain and the range of .
Correct Answer

verified
(a) 
(b) D...View Answer
Show Answer
Correct Answer
verified
(b) D...
View Answer
Essay
Determine whether or not the function is one-to-one.
Correct Answer

verified

is not one-to-one, or sketch ...View Answer
Show Answer
Correct Answer
verified
is not one-to-one, or sketch ...
View Answer
Essay
A function is given. (a) Find all the local maximum and minimum values of the function and the value of x at which each occurs. (b) Find the intervals on which the function is increasing and on which the function is decreasing. State all answers correct to two decimal places.
Correct Answer

verified
(a) local maximum  w...
w...View Answer
Show Answer
Correct Answer
verified
View Answer
Short Answer
A man is running around a circular track that is 200 m in circumference. An observer uses a stopwatch to record the runner's time at the end of each lap, obtaining the data in the following table. What was the man's average speed (rate) between 108 s and 203 s? Round the answer to two decimal places.
Correct Answer

verified
Correct Answer
verified
Essay
Sketch the graph of the piecewise-defined function.
Correct Answer

verified
Correct Answer
verified
Essay
A function is given. Use a graphing calculator to draw the graph of f. Find the domain and range of f from the graph.
Correct Answer

verified
Correct Answer
verified
Essay
For the function , find and .
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Determine whether the given curve is the graph of a function of . If it is, state the domain and range of the function. 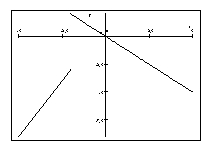
A) Function, domain: , range:
B) Function, domain: , range:
C) Function, domain: , range:
D) Function, domain: , range:
E) Not a function
Correct Answer

verified
Correct Answer
verified
Showing 41 - 60 of 98
Related Exams