A) the Comparison Test and ![]() .
.
B) the Comparison Test and ![]() .
.
C) evaluation of the integral.
D) No method can be used since the function ![]() is not non-negative.
is not non-negative.
E) none of the above.
Correct Answer

verified
Correct Answer
verified
Essay
Use the error bound to find a value of 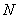 for which
for which  in approximating the integral
in approximating the integral 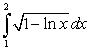 .
.
Correct Answer

verified
Correct Answer
verified
Essay
Evaluate 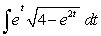 .
.
Correct Answer

verified
Correct Answer
verified
Essay
Approximate the volume of the solid obtained by rotating the graph of 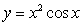 from
from 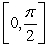 about the line
about the line 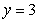 by using
by using 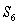 .
.
Correct Answer

verified
Correct Answer
verified
Essay
Evaluate the integral 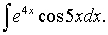
Correct Answer

verified
Correct Answer
verified
Essay
Calculate the following integrals using the reduction formulas when necessary.
A)  B)
B) 
Correct Answer

verified
Correct Answer
verified
Essay
Verify that  has a removable discontinuity at
has a removable discontinuity at 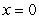 , define
, define 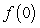 so that
so that  is continuous at 0, and estimate
is continuous at 0, and estimate 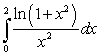 by
by 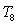 .
.
Correct Answer

verified
Correct Answer
verified
Essay
Verify that 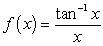 has a removable discontinuity at
has a removable discontinuity at 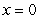 , define
, define 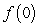 so that
so that 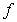 is continuous at
is continuous at 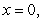 and estimate
and estimate 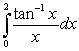 by
by 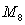 .
.
Correct Answer

verified
Correct Answer
verified
Essay
Verify that 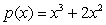 is a probability density function on
is a probability density function on 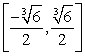 and calculate its mean value.
and calculate its mean value.
Correct Answer

verified
Correct Answer
verified
Short Answer
Evaluate the integral 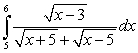 .
.
Correct Answer

verified
Correct Answer
verified
Multiple Choice
To evaluate the integral  by Integration by Parts, the convenient choice is
by Integration by Parts, the convenient choice is
A) ![]()
B) ![]()
C) ![]()
D) ![]()
E) ![]()
Correct Answer

verified
Correct Answer
verified
Essay
Calculate the integral  .
.
Correct Answer

verified
Correct Answer
verified
Essay
Calculate the following integral in terms of inverse hyperbolic functions. 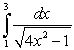
Correct Answer

verified
Correct Answer
verified
Essay
Evaluate the integral 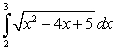 .
.
Correct Answer

verified
Correct Answer
verified
Essay
Evaluate the integral 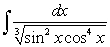 .
.
Correct Answer

verified
Correct Answer
verified
Multiple Choice
To evaluate the integral  using integration by parts, the convenient choice is :
using integration by parts, the convenient choice is :
A) ![]() .
.
B) ![]() .
.
C) ![]() .
.
D) ![]() .
.
E) ![]() .
.
Correct Answer

verified
Correct Answer
verified
Essay
Evaluate 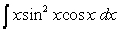 .
.
Correct Answer

verified
Correct Answer
verified
Essay
Evaluate the integral 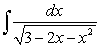 .
.
Correct Answer

verified
Correct Answer
verified
Essay
Evaluate the integral  .
.
Correct Answer

verified
Correct Answer
verified
Essay
Find a constant 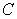 such that
such that 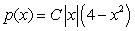 is a probability density on the interval
is a probability density on the interval 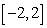 and compute the probability
and compute the probability  .
.
Correct Answer

verified
Correct Answer
verified
Showing 41 - 60 of 101
Related Exams