Asked by
Nicholas Logan
on Nov 26, 2024
Verified
In constructing a 95% confidence interval estimate for the difference between the means of two normally distributed populations, where the unknown population variances are assumed not to be equal, summary statistics computed from two independent samples are: 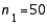 ,
,  ,
, 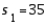 ,
, 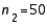 ,
, 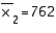 , and
, and 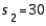 . The upper confidence limit is:
. The upper confidence limit is:
A) 18.78
B) 6.78
C) 5.76
D) 77.3
E) 89.3
Confidence Interval
A confidence interval is a range of values, derived from sample statistics, used to estimate the true value of a population parameter with a certain degree of confidence.
Normally Distributed
Describes a type of continuous probability distribution for a real-valued random variable where the data forms a symmetric, bell-shaped curve about the mean.
Variances Assumed
A condition in statistical analysis where it is presumed that the variances of two or more populations are equal, important in certain tests like ANOVA.
- Differentiate the methods of estimating population parameters based on whether population variances are known or unknown.
- Understand how the size of the sample, the level of confidence, and the variability affect the breadth of confidence intervals.

Verified Answer
CM

Learning Objectives
- Differentiate the methods of estimating population parameters based on whether population variances are known or unknown.
- Understand how the size of the sample, the level of confidence, and the variability affect the breadth of confidence intervals.